但是真正做好一件事没有捷径,需要一万小时的专业训练和努力。 ———— 《数学之美》
<1>关于搜索引擎
1.搜索引擎的组成
在《数学之美》中,吴军博士把搜索引擎的关键提炼成了3个方面:
1.下载 ———— 通过网路爬虫实现 。搜素引擎的网络爬虫问题应该定义成“如何在有限的时间内最多地爬下最重要的网页”。首先,各个网站中最重要的网页肯定是首页,所以在这个前提下,广度搜索(BFS)明显优于深度搜索(DFS)。而实际的网络爬虫都是由成千上万的服务器组成的,对于一个网站,需要一次性把这个网站的内容都下载下来,而不是先下载5%,然后到第二轮再继续下来,所以这个就有点类似于(DFS)。这个的原因和爬虫的分布式结构以及网络通信的握手成功成本有关。同时,爬虫对网页遍历的次序不是简单的BFS或者DFS,所以就需要一个相对复杂的下载优先级排序的方法,这个管理优先级的子系统一般成为调度系统。
2.索引 ———— 搜索引擎能在极短的时间内找到成千上万的搜索结果,是通过索引的方法来实现的。最简单的索引 就是对于一个确定的关键字,用01来表示一篇文章或者一个网页是否含有这个关键字,但是这样有多少个网页或者多少篇文章,这个二进制数就有多少位。虽然计算机处理二进制数的速度很快,但是由于这个索引十分庞大,这就需要把索引分成很多份,分别存储在不同的服务器中。没当接受一个查询的时候,这个查询就被分发到这些不同的服务器上,并行的处理请求,然后再把结果发送到主服务器中进行合并处理,最后返回给用户。
3.排序 ————PageRank算法 。Google的PageRanke算法由佩奇和布林发明。这个算法的思想 在于民主表决,Y的网页排名pagerank来源于指向这个网页的所有网页X1、X2...Xk的权重之和。其中佩奇认为,X1、X2...Xk的权重分别是多少,这个取决去这些网页本身的排名。但是这就成为了一个先有鸡,还是先有蛋的问题。而解决这个问题的是布林,他把这个问题变成了一个二维矩阵相乘的问题,并且用迭代的方法解决了这个问题。他们先假定所有网页的排名都是一样的,并且根据这个初始值进行不断的迭代。从理论上证明,无论初始值如何选取,这种算法都保证了网页排名的估计值能收敛到排名的真实值,而且这个排名是没有任何人工干预的。在理论上,这个二维矩阵的元素有网页数量的平方那么多,计算量是非常庞大的,而佩奇和布林利用稀疏矩阵计算的技巧,大大简化了计算量,实现了这个网页排名算法。计算量仍然十分庞大,所以Google的工程师发明了MapReduce这个并行计算工具,使得PageRank的并行计算完全自动化。
2.搜索技术——有限状态机
在《数学之美》中还提到了本地搜索的最基本技术——有限状态机。 举一个例子就是要搜索一个地址,这就需要判断一个地址的正确性,同时非常准确地提炼出相应的地理信息(省、市、街道等)。这就就需要一个有限状态机来完成,有限状态机是一个特殊的有向图,有一个开始状态和一个终止状态,就比如开始是“XX省”,然后一个箭头既可以指向“XX市”,也可以指向“XX县”,但是不能是从“XX市”指向“XX省”,这里面具体的实现算法书中也并没有提到。
3.搜索中的最短路径问题
在这之后还提到了一个就是全球导航和动态规划(Dynamic Programming)的问题。就是要找出两个点之间的最短距离问题。当然这个最短距离是带有权重的,比如说花费的时间,消耗的金钱等等。
举一个例子就是从北京到广州的最短路径,这时候可以把北京—>广州的最短路径拆成从北京—>石家庄和石家庄—>广州这两条路径,当这两条路径都是最短的时候,整体的路径就都是最短的。但是可能会有疑问就是北京—>广州的路径就一定经过石家庄吗?这个问题可以变成图论中的最小割问题(吐槽图论老师1万字省略。。。),没学过的可以想像一下,把你双手的五个手指张开,并左右手按手指顺序把手指尖碰在一起,这时从你左手臂到右手臂的这条路径中,肯定都会经过大拇指、食指、中指、无名指、小拇指之中的其中一个,都由这五个手指组成的点或者边就是图论里面的最小割集或者最小边集(比喻不是很恰当)。这时候打个比方,北京到广州的最短路径,就肯定会经过石家庄、天津、太原、郑州和武汉这五个城市中的其中一个,然后继续下去寻找局部的最短路径,就可以大大降低最短路径的计算复杂度。
<2>TF-IDF、聚类问题
1.TF-IDF是什么
在《数学之美》中提到了如何确定一个网页和某个查询的相关性,而这个搜索关键词权重的科学衡量指标就是TF-IDF(Term-frequency/Inverse Document Frequency),即词频/逆文本频率指数。
其中TF指的是关键词的频率,比如说一个“原子能”的词在一个共有1000个词的网页上出现了2词,那么“原子能”的词频就是0.002,所以是多个词组成的关键词,就是把这些关键词的TF相加
其中IDF指的是就是关键词的权重,比如“原子能的应用”中,“原子能”的权重要大于“的”和“应用”的权重,公式为log(D/Dw),其中D是全部网页的个数,如果“的”在所有网页中都出现了的话,那么“的”的权重就是log(1)=0,这样就能对于不同的关键词有不同的权重。2.新闻分类(聚类问题)和余弦相似度
除了搜索中评价网页和某个查询的相关性中用到TF-IDF,在新闻的分类,或者说聚类问题中,也用到了TF-IDF。把某一则新闻中所有的词算出的TF-IDF,按它的在词汇表中出现顺序进行排列,就可以得到一个向量。比如说词汇表共有64000个词,那么没有出现的词的TF-IDF就是0,而这个向量就是这一则新闻的特征向量(Feature Vector)。这时候,就可以利用余弦定理来计算两则新闻之间的夹角,而这个余弦的值就是两则新闻的相关度,即余弦相似性。越小表示两则新闻越相关,就越可以分在一类;如果算出来夹角是90度,那么就说明这两则新闻完全不相关,余弦公式:
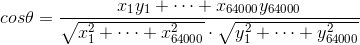
3.奇异值(SVD)分解
这样就可以根据余弦相似性的值设定阈值来对新闻进行分类。然而在计算的过程中,由于计算量很大,这是需要借助矩阵论的知识对这些计算量进行优化。在成千上万的新闻和百万的词汇表的计算中(比如说矩阵的每一一行代表词汇表中的每一个词,矩阵的每一列代表一则新闻),要计算每一列新闻中两两之间的余弦相似度,就要进行奇异值分解(SVD分解),如果有N个词和M篇文章,这就是一个MN的矩阵,此时M=1000000,N=500000,就是100万50万,总共5000亿个元素。通过SVD分解,就能把这个大矩阵分解成一个100万100的矩阵X,一个100100的矩阵B,和一个100*50万的矩阵Y,这三个矩阵相乘的结果。这三个矩阵的元素共和为不超过1.5亿,计算量和存储量会大大减小。而这三个分解出来的矩阵也有非常清晰的物理含义,举个例子:
—————————A矩阵——————————— X矩阵 ————— B矩阵 —————— Y矩阵

其中X矩阵的每一行表示一个词,每一列表示一个语义相近的词类
其中B矩阵表示词的类和文章的类之间的相关性 其中Y矩阵是对文本的分类结果,每一行对应一个主题,每一列对应一个文本4.相似哈希和信息指纹
当然余弦相似度还可以用于对比信息指纹的重复性,《数学之美》中还提到了相似哈希这个特殊的信息指纹,具体的计算方法可以去看《数学之美》P150页。 相似哈希的特点就是,如果两个网页的相似哈希相差越小,这两个网页的相似性越高;如果两个网页相同,则相似哈希肯定相同;如果少数权重小的词不同,其余的都相同,相似哈希也会几乎相同。之所以看到相似哈希会有印象,也是由于上次参加的某个算法比赛中对作弊的代码进行筛选的时候,主办方就用的相似哈希这个评价标准,所以对于常见的跨语言作弊、替换变量名作弊的方法都能进行有效的识别。
5.K-mean算法
《数学之美》中提到聚类问题的时候,还提到了期望最大化算法,也就是K-means算法。
K-means算法是随机地挑出出一些类的中心,然后来优化这些中心,使得它们和真实的聚类中心尽可能一致。假设有N篇文章,我们想把它们分成K类,这时我们可以不知道K具体是多少,最终分成多少类就分成多少类。
K-means算法的步骤是:
1.随机挑选K个点作为起始的中心; 2.计算所有点到这些聚类中心的距离(使用欧几里德公式),将这些点归到最近的一类中; 3.重新计算每一类的中心; 4.迭代,最终偏移非常小的时候得到收敛。 这一类算法的过程中,根据现有的模型,计算各个观测数据输入到模型中的计算结果,这个过程成为期望值计算过程,即E过程;接下来,重新计算模型参数,以最大化期望值,这一过程称为最大化的成果,即M过程。这一类算法都称为EM算法。<3>关于最大熵原理
最大熵原理指出,需要对一个随机事件的概率分布进行预测的时候,我们的预测应当满足全部已知的条件,而对未知的情况不要做任何的主观假设。在这种情况下,概率分布最均匀,预测的风险最小。因为这时概率分布的信息熵最大,所以人们称这种模型叫做“最大熵模型”。即“不要把所有的鸡蛋放在一个篮子里”,因为当我们遇到不确定性的时候,就要保留各种可能性。
<4>关于机器学习和自然语言处理
1.图灵和人工智能
机器学习(Machine Learning)是一门专门研究计算机怎样模拟或者实现人类的学习,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能的学科。而最早提出机器智能设想的是计算机科学之父—————阿兰·图灵(Alan Turing)。他在1950年的《思想》杂志上发表了一篇题为“计算的机器和智能”的论文中,提出了一种验证机器是否有智能的方法:让人和机器进行交流,如果人无法判断自己交流的对象是人还是机器的时候,就说明这个机器有了智能。后来这种方法被成为图灵测试(Turning Test)。
2.自然语言处理的历史
而在自然语言的机器处理(自然语言处理)的历史中,可以分成两个阶段:
1.一个是20世纪50年代到70年代,也就是从大约1950-1970的这段时间,全世界的科学家对计算机处理自然语言的认识都被自己局限在人类学习语言的方式上,就是用计算机模拟人脑。后面吴军博士提到了这段时间对自然语言处理的研究主要是基于规则的方式,想让计算机完成翻译或者语音识别这样只有人类才能完成的事情,就必须先让计算机理解自然语言,即让计算机有类似人类这样的智能。比如学习语言的过程中要学习语法规则,词性和构词法等等,而这些规则有很容易用算法来描述,所以在当时大家对基于规则的自然语言处理很有信心。但是实际上,当用算法来描述这些规则的时候,所形成的语法分析树十分的复杂,而且规则的数量众多,耗时且有时会互相矛盾。所以在20世纪70时代,基于规则的句法分析走到了尽头,也使得这段时间的成果近乎为零。
2.另一个阶段是20世纪70年代后,一些先驱认识到基于数学模型和统计的方法才是正确的道路,所以自然语言处理进入了第二个阶段。这种方式的思想在于统计,即大多数样本怎么做。
举个例子就是:pen有两个意思,一个意思是钢笔,而另一个意思是围栏。对于两个句子“The pen is in the box.”和“The box is in the pen.”来说,正确的翻译应该是“钢笔在盒子里。”和“盒子在围栏里。”,因为正常来说,盒子是不可能在钢笔里的。在20世纪70年代,给予统计的方法的核心模型是通信系统加隐含马尔可夫模型。这个系统的输入和输出都是一维的符号序列,而且保持原有的次序。最高获得成功的是语音识别是如此,后来第二个获得成功的此词性分析也是如此。而在句法分析中,输入的是一维的句子,输出的是二维的分析树;在机器翻译中,虽然输出的依然是一维的句子,但是次序会有很大的变化,所以上述的方法就不太管用了。1988年,IBM的彼得·布朗(Peter Brown)等人提出了基于统计的机器翻译方法,框架是正确的,但是由于缺乏足够的统计数据和没有足够强大的模型来解决不同语言语序颠倒的问题,所以实际的效果很差,后来这些人去了文艺复兴公司发财去了。而只有出现了基于有向图的统计模型才能很好的解决复杂的句法分析这个问题。
<5>提到的计算机领域的科学家
1.阿兰·图灵(Alan Turing)————计算机科学之父 2.约翰·麦卡锡(John McCarthy)————图灵奖获得者,发明Lisp语言,斯坦福大学人工智能实验室的主任 3.马文·明斯基(Marvin Minsky)————图灵奖获得者,创建麻省理工学院(MIT)人工智能实验室 4.纳撒尼尔·罗切斯特(Nathaniel Rochester)————IBM的杰出计算机设计师 以上四人于1956年在达特茅斯学院举办的夏季人工智能研讨会是计算机科学史上的一座里程碑,参加会议的包括下面两位,总共10人。讨论了当时计算机科学尚未解决的问题,包括人工智能、自然语言处理和神经网络等。 5.赫伯特·西蒙(Herbert Simon)————图灵奖获得者,同时还是美国管理学家和社会科学家,经济组织决策管理大师,第十届诺贝尔经济学奖获奖者 6.艾伦·纽维尔(Allen Newell)————图灵奖获得者 7.高德纳·克努特(Donald Knuth)————图灵奖获得者,算法和程序设计技术的先驱者,计算机排版系统TEX和METAFONT的发明者,提出用计算复杂度来衡量算法的耗时 8.弗里德里克·贾里尼克(Frederick Jelinek)————领导IBM华生实验室,提出采用统计的方法解决语音识别问题 9.米奇·马库斯(Mitch Marcus)————设立和领导了LDC项目,采集和整理全世界主要语言的语料(其中著名的是Penn Tree Bank),并培养了一批世界级的科学家
<6>统计语言模型
计算机处理自然预言,一个基本的问题就是为自然语言这种上下文相关的特性建立数学模型。这个数学模型就是在自然语言处理中常说的统计语言模型。
1.怎样求一个句子S合理的可能性
贾里尼克的思想就是:认为一个句子是否合理,就是看它的可能性大小如何。 假定S表示某一个有意义的句子,由一连串特定顺序排列的词w1、w2...wn组成,这里n是句子的长度。其中S出现概率是:
2.一个句子S合理的可能性和句中每个词都有关
利用条件概率公式: 得:
其中,P(w1)是第一个词出现的概率,P(w2|w1)是在已知第一个词的前提下,第二个词出现的概率,到了第n个词,这个词出现的概率和前面所有的词出现的概率都有关。
3.马尔可夫假设:后一个出现的概率只和前一个词有关(条件概率)
计算第一个词出现的概率很简单,即P(w1),第二个词的条件概率P(w2|w1)很是可以计算的,但是越到后面,计算量就越来越大。到了19世纪至20世纪初的这段时间,俄罗斯有一个数学家——马尔可夫(Andrey Markov)就提出了方法,就是遇到这种情况,就假设任意一个词Wi出现的概率只和前面一个词Wi-1有关。这种假设在数学上成为马尔可夫假设。这下公式变成: 以上这个公式对应了统计语言模型中的二元模型(Bigram Model)。
4.如何计算条件概率——分别计算联合概率和边缘概率
接下来的问题变成了如何计算条件概率
当要计算联合概率P(Wi-1,Wi)和边缘概率P(Wi-1)的时候,需要大量的机读文本,也就是语料库。其中
根据大数定理,当统计量足够充分的时候,相对频度就等于概率,即
5.高阶模型的计算量
对于高阶语言模型,是假定文本中的每个词都和前面的N-1个词有关,而和更前面的词无关。对于N元模型的空间复杂度,几乎是N的指数函数O(|V|^N),时间复杂度也是一个指数函数,O(|V|^N-1).所以N的大小决定了空间复杂度和时间复杂度的大小。当N从1到2,从2再到3的时候,模型的效果上升的很明显,但是从3到4的时候,效果的提升就不是很显著了。
模型训练中的问题:
零概率问题——假定要训练一个汉语的语言模型,汉语的词汇量大致是20万这个量级,训练一个3元模型就需要200000^3 = 8*10^15这么多的参数,但是由于训练数据量不可能达到这么多,所以如果用直接的比值计算概率,大部分的条件概率依然是零,这种模型我们称之为“不平滑”。对于这种问题,图灵提出了一种在统计中相信可靠的统计数据,而对不可信的统计数据大折扣的一种概率估计方法,同时将折扣出来的那一小部分概率给予未看见的事件。这个重新估算概率的公式后来被称为古德-图灵估计。<7>隐含马尔可夫模型
1.已经求出一个句子S出现的概率
当求出了一个句子S出现概率之后:
2.在已知一个英文句子O出现概率的情况下,求汉语句子S出现概率最大的那个S,即O最有可能被翻译成S(机器翻译)
对于一个观测到的信号o1,o2,……,on来还原发送的信号s1,s2,……,sn,实际的例子可以是根据收到的英文,求原来汉语的意思,这就是机器翻译的原理。写成数学表达式就是求以下公式有最大值时候的那个s1,s2,s3……:
3.利用贝叶斯公式化简
利用贝叶斯公式,可以把上述公式转换成(把条件概率公式用了两次):
其中P{s1,s2,s3,……|o1,o2,o3,……}表示信息s1,s2,s3,……在传输之后变成接收的信号o1,o2,o3,……的可能性;
而P{s1,s2,s3,……}表示s1,s2,s3,……本身是一个在接收端合乎情理的信号的可能性;最后而P{o1,o2,o3,……}表示在发送端产生信息o1,o2,o3,……的可能性(注意s和o在经过了条件概率公式后交换了发送和接收的位置),这时由于P{o1,o2,o3,……}是一个可以忽略的常熟,所以上面公式等价于4.再次利用马尔可夫假设(转移概率)
这时,可以用隐含马尔可夫模型来解决这个问题:隐含马尔可夫模型其实并不是19世纪俄罗斯数学家马尔可夫发明的,而是美国数学家鲍姆等人在20世纪六七十年代发表的一系列论文中提出的,隐含马尔可夫模型的训练方法(鲍姆-韦尔奇算法)也是以他的名字命名的。隐含马尔可夫模型之所以是隐含的,是因为它每一个时刻的状态是不可见的。而对于马尔可夫链来说,对于一个随机时间序列S1,S1,S3,……St中的每一个状态的概率,不只其本身是随机的,也就是说它可以是马尔可夫链中的任何一个状态,而且它还和前一个状态有关,这两点说明了St的概率有两个维度的不确定性。在任一时刻t的状态St是不可见的且是不确定的,因为这时候只知道输出的序列Ot,所以观察者不能通过观察到s1,s1,s3,……sr来推测转移概率等参数。但是可以通过Ot来推测这些参数。 此时根据上节马尔可夫提出的只和前一个有关的假设: 所以,可得
其中P{s1,s2,s3,……}就是上一节求出的每一个句子是否合理的可能性,也就是从收到的英文{O1,O2,O3,……}求原来的汉语{S1,S2,S3,……}的过程中,这个汉语句子{s1,s2,s3,……}存在的合理性。可以理解为“The box is in the pen”被翻译成“盒子在钢笔中”和“盒子在围栏中”这两个句子哪个更合理。 而P{s1,s2,s3,……|o1,o2,o3,……}根据应用的不同而有不同的名称,在语音识别中被成为“声学模型”,在机器翻译中是“翻译模型”,而在拼写校正中是“纠错模型”。
5.如何求转移概率和生成概率
此时,问题变成了求转移概率和生成概率乘积的最大值的问题1.转移概率 其中N(St-1)就是在有了足够多的人工标记的数据后,经过状态St-1的次数(可以理解为在语料库中某个词St-1出现的次数),而N(St-1,St)是在经过St-1这个状态后转移到St这个状态的次数(可以理解为在语料库中词St-1后出现词St的次数),而这两个数的比值就是转移概率P(St|St-1)的值 同理2.生成概率
其中N(St)就是在有了足够多的人工标记的数据后,经过状态St的次数(可以理解为在语料库中某个词St出现的次数),而N(Ot,St)是在经过Ot这个状态后转移到St这个状态的次数(可以理解为在语料库中英文单词Ot被翻译成汉语词语St的次数),而这两个数的比值就是生成概率P(Ot|St)的值
6.如何求转移概率和生成概率乘积的最大值
当求出转移概率和生成概率之后,就能求出一个已知的英文句子{O1,O2,O3,……}被翻译成{S1,S2,S3,……}的所有可能性的大小,然后下一步就是要求这所有的可能性中最大的时候的那个{S1,S2,S2,……},这需要用到维特比算法。维特比算法是一个动态规划算法,在求所以可能性中最大的值的时候,也相当于求一个求概率最大的路径(或者最短路径)的问题。在已知输出的英文{O1,O2,O3,……}的情况下,可能有很多种不同的路径能从而得到不同的中文{S1,S2,S3,……},这些路径组成了一个成为篱笆网络(Lattice)的图,其中我们要求的是最可能的,也就是概率最大的那个中文{S1,S2,S3,……}。 举个例子就是Bush可以翻译成布什,也可以翻译成灌木丛,但是当Bush的前一个词是总统的时候,Bush翻译成布什的概率最大。这时就可以参考从北京到广州的最短路径的问题,使用维特比算法对计算量进行化简。
有监督的训练需要大量人工标记的数据,实际上很多应用不可能做到,就翻译模型的训练来说,这需要大量的中英文对照的语料,还要把中英文词语一一对应起来。所以在实际的训练中常常使用的是无监督的训练算法,即鲍姆-韦尔奇算法。鲍姆-韦尔奇算法的思想是首先寻找一组能够产生输出序列O的模型参数,这个模型是一定存在的,因为当转移概率P和输出概率Q为均匀分布的时候,模型可以产生任何输出。然后在这个模型的基础上算出这个模型产生输出序列O的概率,并根据这个模型可以找到一个更好的模型,这个新的模型输出序列O的概率大于原来的模型。经过了不断的迭代从而不断的估计新的模型参数,使得输出序列O的概率最大化。这个过程被称为期望最大化(Expectation-Maximization),简称EM过程。
具体的方法和公式《数学之美》中并没有细说,具体的过程就没能理解了。